Function Pyramids

This problem extends the ideas explored in Number Pyramids and More Number Pyramids.
 
A function pyramid is a structure where each entry in the pyramid is determined by the two entries below it, together with some function:
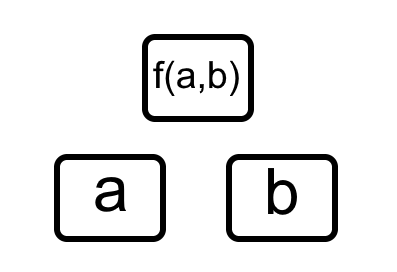The function used in the problems Number Pyramids and More Number Pyramids could be expressed as: $$f(a,b) = a+b$$
 
Here is a function pyramid for you to explore. Select numbers for the three spaces on the bottom layer, and look at how the rest of the numbers change. If you are using a mobile phone, you may need to rotate your screen to landscape orientation.

Can you work out the function that determines the middle and top layers of the pyramid? 
 
 
Here are some questions you might like to consider:
 
Can you choose numbers for the bottom layer so that the number 1 appears in the top cell?
Can you do it in more than one way?

Can you choose numbers for the bottom layer so that the number 5 appears in the top cell?
Can you do it in more than one way?

Can you choose numbers for the bottom layer so that the numbers in the middle layer are negative?
Can you choose numbers for the bottom layer so that the number in the top cell is negative?