Skip over navigation
Sam Yun from Sri Kdu International School in Malaysia and Daskesh from Hymers College in the UK tried some numbers systematically. This is Sam Yun's work:
For simplicity, we will keep 1 value constant whilst changing the other value. We will start by keeping the number '1' constant. Then, we can change the other value by adding '1' to it each time.
Test 1: Input = 1, 1 Output = 0
Test 2: Input = 1, 2 Output = 1
Test 3: Input = 1, 3 Output = 1.58...
Test 4: Input = 1, 4 Output = 2
Now, repeat this with a different constant.
Test 5: Input = 2, 2 Output = 2
Test 6: Input = 2, 3 Output = 2.58...
Test 7: Input = 2, 4 Output = 3
Test 8: Input = 2, 5 Output = 3.32...
From these few tests, we can see that the outputs are either whole numbers or decimals. Because it is hard to identify patterns from decimal outputs, we can ignore those tests and only focus on the tests that outputs whole numbers.
List of inputs that outputs whole numbers:
1 & 1 1 & 2 1 & 4 2 & 2 2
& 4
Possible relationship(s):
- Powers of 2 (1 = 2^0, 2 = 2^1...)
Dakshesh also focused on the powers of 2:

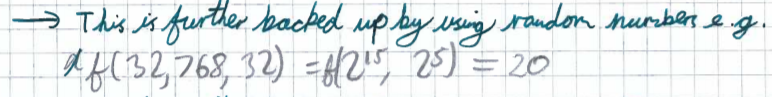
Matthew from the UK noticed a different pattern in the numbers:
2 positives gave a positive outcome
1 positive and 1 negative gave no outcome
2 negatives gave a positive outcome.
This led me to think that there was either a multiplication or division going on between the 2 numbers, since the 2 negatives multiplied/divided would output a positive number.
Then, since the function was clearly undefined for those inputs $(a,b)$ where $ab<0$, then there are a few common functions which hold this property.
From this observation, Florence from Roedean School in the UK, Agathiyan from Hymers College in the UK in the UK and Matthew worked out what the function $f$ was. Deepak from Macmillan Academy in the UK explained what the function does:
Multiply the two input numbers below the number which is the output and $2^{\text{output}} = \text{input}\times\text{input}$
Agathiyan from Hymers Dakshesh, Sum Yun, Florence, Matthew and Agathiyan wrote this as:
$f(a,b) = \log_2{a} + \log_2{b}$, which is equal to $\log_2{ab}$
Dakshesh went on to express the numbers in the pyramid in terms of the numbers at the bottom, and to find out whether it is possible to get negative numbers in the middle or top layers:
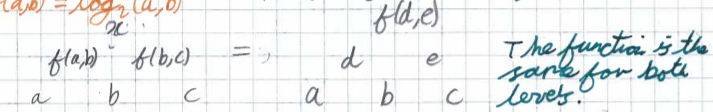






Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Function Pyramids
Age 16 to 18
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Sam Yun from Sri Kdu International School in Malaysia and Daskesh from Hymers College in the UK tried some numbers systematically. This is Sam Yun's work:
For simplicity, we will keep 1 value constant whilst changing the other value. We will start by keeping the number '1' constant. Then, we can change the other value by adding '1' to it each time.
Test 1: Input = 1, 1 Output = 0
Test 2: Input = 1, 2 Output = 1
Test 3: Input = 1, 3 Output = 1.58...
Test 4: Input = 1, 4 Output = 2
Now, repeat this with a different constant.
Test 5: Input = 2, 2 Output = 2
Test 6: Input = 2, 3 Output = 2.58...
Test 7: Input = 2, 4 Output = 3
Test 8: Input = 2, 5 Output = 3.32...
From these few tests, we can see that the outputs are either whole numbers or decimals. Because it is hard to identify patterns from decimal outputs, we can ignore those tests and only focus on the tests that outputs whole numbers.
List of inputs that outputs whole numbers:
1 & 1 1 & 2 1 & 4 2 & 2 2
& 4
Possible relationship(s):
- Powers of 2 (1 = 2^0, 2 = 2^1...)
Dakshesh also focused on the powers of 2:
Matthew from the UK noticed a different pattern in the numbers:
2 positives gave a positive outcome
1 positive and 1 negative gave no outcome
2 negatives gave a positive outcome.
This led me to think that there was either a multiplication or division going on between the 2 numbers, since the 2 negatives multiplied/divided would output a positive number.
Then, since the function was clearly undefined for those inputs $(a,b)$ where $ab<0$, then there are a few common functions which hold this property.
From this observation, Florence from Roedean School in the UK, Agathiyan from Hymers College in the UK in the UK and Matthew worked out what the function $f$ was. Deepak from Macmillan Academy in the UK explained what the function does:
Multiply the two input numbers below the number which is the output and $2^{\text{output}} = \text{input}\times\text{input}$
Agathiyan from Hymers Dakshesh, Sum Yun, Florence, Matthew and Agathiyan wrote this as:
$f(a,b) = \log_2{a} + \log_2{b}$, which is equal to $\log_2{ab}$
Dakshesh went on to express the numbers in the pyramid in terms of the numbers at the bottom, and to find out whether it is possible to get negative numbers in the middle or top layers:
You may also like
Modular Fractions
We only need 7 numbers for modulus (or clock) arithmetic mod 7 including working with fractions. Explore how to divide numbers and write fractions in modulus arithemtic.
Readme
Decipher a simple code based on the rule C=7P+17 (mod 26) where C is the code for the letter P from the alphabet. Rearrange the formula and use the inverse to decipher automatically.
Double Time
Crack this code which depends on taking pairs of letters and using two simultaneous relations and modulus arithmetic to encode the message.

