Pair Products
Pair Products printable worksheet
Choose four consecutive whole numbers.
Multiply the first and last numbers together.
Multiply the middle pair together.
Choose several different sets of four consecutive whole numbers and do the same.
What do you notice?
Can you explain what you have noticed? Will it always happen?
Click below to see how Charlie and Alison explained what they noticed.
Charlie said:
I can explain this by labelling the four consecutive numbers $n, n+1, n+2, n+3$.
Outer pair: $n(n+3) = n^2 + 3n$
Inner pair: $(n+1)(n+2) = n^2 + 3n + 2$
Alison said:
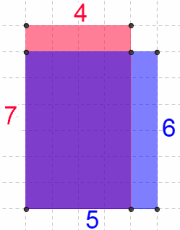
I drew a diagram, in which the product of each pair is represented by the area of a rectangle:
The outer pair is represented by the red rectangle.
The inner pair is represented by the blue rectangle.
The purple area is common to both.
The area of the red strip will always be two units less than the area of the blue strip.
Therefore, the product of the outer pair is always two less than the product of the inner pair.
Instead of doing lots of calculations, can you use these representations to compare the product of the first and last numbers with the product of the second and penultimate numbers, when you have:
- $5$ consecutive whole numbers
- $6, 7, 8, \ldots x$ consecutive whole numbers
- $4$ consecutive even numbers
- $4$ consecutive odd numbers
- $5, 6, 7, 8, \ldots x$ consecutive even or odd numbers
- $4$ consecutive multiples of $3, 4, 5 \ldots $
- Decimals that differ by $1$, such as $1.2, 2.2, 3.2, 4.2$
- Four numbers going up in $3$s, such as $2, 5, 8, 11$
- Four numbers going up in $\frac{1}{2}$s, such as $4, 4\frac{1}{2}, 5, 5\frac{1}{2}$
Make up a few similar questions of your own. Impress your friends by giving them a calculator and 'predicting' what will happen!
You may also like
DOTS Division
Take any pair of two digit numbers x=ab and y=cd where, without loss of generality, ab > cd . Form two 4 digit numbers r=abcd and s=cdab and calculate: {r^2 - s^2} /{x^2 - y^2}.
Sixational
The nth term of a sequence is given by the formula n^3 + 11n. Find the first four terms of the sequence given by this formula and the first term of the sequence which is bigger than one million. Prove that all terms of the sequence are divisible by 6.