Skip over navigation
This problem could also be approached purely numerically, as an exercise in developing fluency with multiplication tables while looking for pattern and structure.
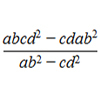

Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
Advanced mathematics
For younger learners
Pair Products
Age 14 to 16
Challenge Level 





- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Why do this problem?
This problem provides a purpose for practising the routine algebraic procedure of expanding brackets.
For students who are unfamiliar with algebra, this problem is an excellent context for observing, conjecturing and thinking about proof. It can be a good introduction to the power of algebra, and to a related geometrical interpretation.
Possible approach
"Choose four consecutive numbers, multiply the outer pair and the inner pair. What were your two answers?"
Write a selection of students' responses on the board.
"What do you notice?" The inner pair product is always two more than the product of the outer pair.
"Will this always happen? Can you explain why?"
Give students some time to discuss with their partner why the answers always differ by two. Circulate and listen out for interesting insights.
Bring the class together and share any explanations they have found. Perhaps share Charlie's and Alison's representations from the problem if they haven't emerged.
"We've worked out what happens when you find the product of the inner and outer pair of a set of four consecutive numbers. What questions do you think a mathematician might ask next?"
Write students' suggestions up on the board. If suggestions are not forthcoming, introduce some of the ideas listed in the problem.
"You should be able to work out what will happen in the situations you've suggested using one of the powerful representations we've looked at, without having to try out lots of numerical examples first. Of course, if you want, you can use a numerical example to verify what you've done."
Students could be offered a choice of which situations to work on. Alternatively, you may want everybody to work on a series of related problems (5, 6, 7 ... n consecutive numbers, for example) that will lead to a generalisation.
One nice plenary activity is to challenge students to work out quickly what the difference in pair products will be for a randomly chosen sequence of numbers.
Key question
Is there a way to represent the pair products that will explain the patterns you noticed?
Possible support
This problem could also be approached purely numerically, as an exercise in developing fluency with multiplication tables while looking for pattern and structure.
In getting started, there is a dynamic image of Alison's representation that could be used to help students to see why the difference will always be 2.
Possible extension
This problem only operated on the end numbers and the 'end but one' numbers. Invite students to generalise further by looking at other pairs within the sequence.
For example, if you have an odd number of consecutive numbers, what's the difference between the product of the end numbers and the square of the middle number?
You may also like
DOTS Division
Take any pair of two digit numbers x=ab and y=cd where, without loss of generality, ab > cd . Form two 4 digit numbers r=abcd and s=cdab and calculate: {r^2 - s^2} /{x^2 - y^2}.
Sixational
The nth term of a sequence is given by the formula n^3 + 11n. Find the first four terms of the sequence given by this formula and the first term of the sequence which is bigger than one million. Prove that all terms of the sequence are divisible by 6.

