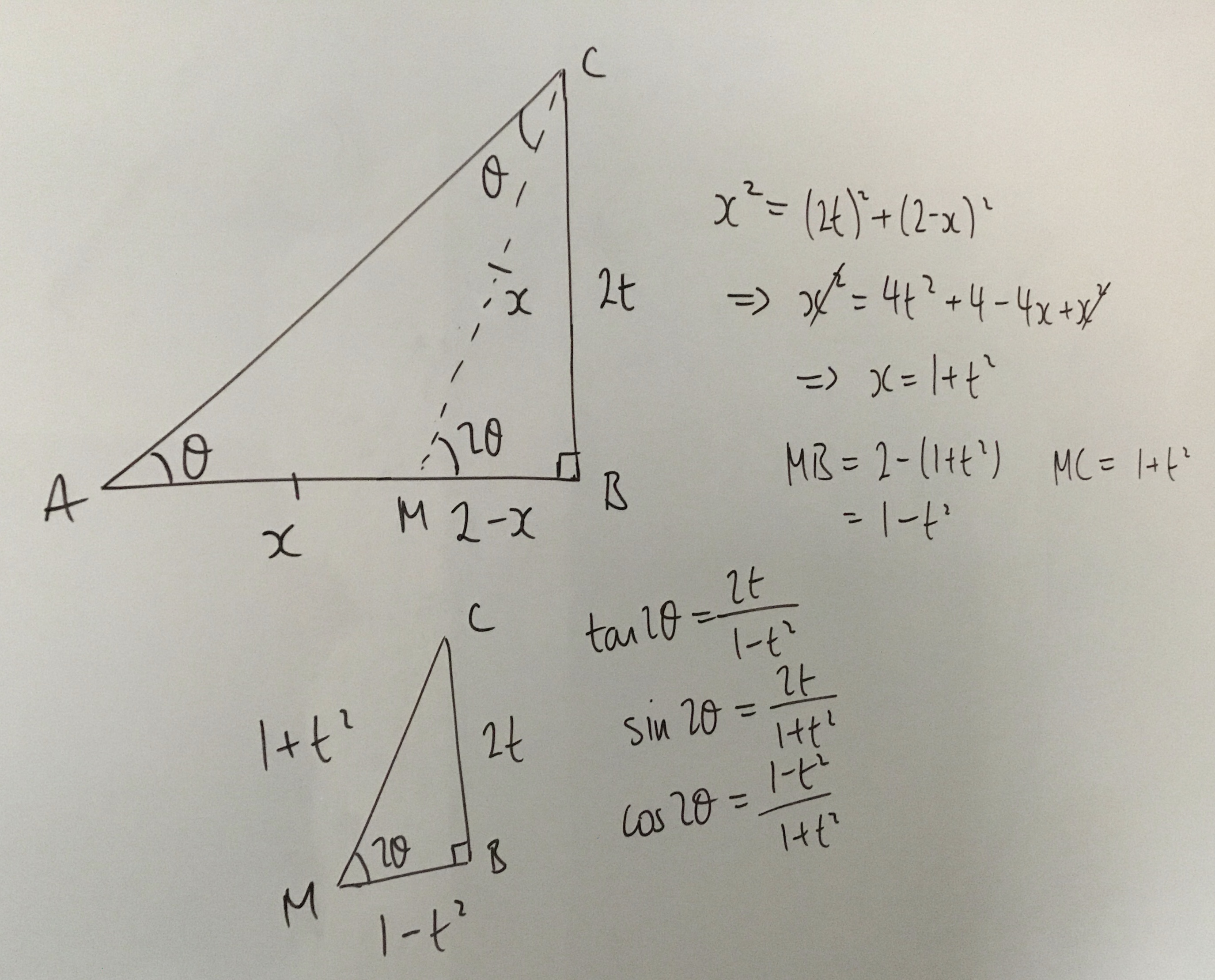T for Tan

Well done to Dylan from Brooke Weston, Joshua from Bohunt Sxth Form, Mykhailo and Daniel, Ilan, Adam and Alexander from JFS, Soumya from King's Maths School, Josh from Queen Elizabeths Grammar School Alford, Bertie from Sir William Borlase's Grammar School, Isy and Rafi, all in the UK, and to DongYeon, who all used Pythagoras' Theorem first to solve the problem. Here is Dylan's work:

Three mathematicians from Simon Balle All-through School wrote a two-page paper explaining their work. They used a slightly different method. You can download their paper here.

DongYeon suggested generalising the problem:

This will work for any right triangle of any length. Let's use a variable $L$ instead of $2.$

$h = L\tan \theta$
 

$(Lt)^2 + (L - x)^2 = x^2$

$x = \dfrac{L(1 + t^2)}2$

$L - x = \dfrac{L(1 - t^2)}2$
 

$\tan{2\theta} = \dfrac h{(L - x)} = \dfrac{Lt}{\frac{L(1 - t^2)}{2}} = \dfrac{2t}{1 - t^2}$

$\sin{2\theta} = \frac hx = \dfrac{Lt}{\frac{L(1 + t^2)}{2}} = \dfrac{2t}{1 + t^2}$

$\cos{2\theta} = \dfrac{L - x}x = \dfrac{\frac{L(1 - t^2)}2}{\frac{L(1 + t^2)}{2}} = \dfrac{1 - t^2}{1 + t^2}$

Note that this is not necessary: using $2$ rather than $L$ did not mean that $\tan{2\theta}=\dfrac{2t}{1 - t^2}$ is only true for triangles where one side is less than $2$. It is true for all acute values of the angle $\theta .$ So in this case, you can prove the formula using a side of length $L,$ or of any other length. When this is the case, it is often most efficient to choose a simple number, like $1$ or $2.$