Skip over navigation
Students will need to be familiar with the operations introduced in Twisting and Turning:
Twist ($x \mapsto x+1$) and Turn ($x \mapsto -\frac1x$).
These notes assume that students will have worked on More Twisting and Turning, and developed a general strategy to get to zero, from any fraction. This problem uses T to represent Twist, and R (for rotate) to represent Turn.
Set the first challenge:
Give students some time to work on this, perhaps using the interactive tool in Getting Started to check their work. Then discuss their strategy and justification for getting fractions of the form $\frac{n}{n+1}$.
Then set the next challenge, asking students to try the following sequences:
For students who have met proof by induction, this could be a good opportunity to use that strategy.
The final part of the problem suggests students look for ways to make any fraction, starting from zero. This is quite challenging; the key questions below might provide a useful prompt.
Can you find a strategy to get from any fraction to zero using an inverse twist and a turn function?
How does that help you get from zero to your chosen fraction using the original twist and turn functions?
All Tangled Up
Age 14 to 18
Challenge Level 
Why do this problem?
This problem follows on from Twisting and Turning and More Twisting and Turning and offers students the opportunity to explore sequences of fractions, make generalisations, and prove conjectures. The rope trick in the first problem offers a moment of surprise when the rope becomes untangled, and this prompts curious students to want to explain what is going on. This third problem in the sequence ties up all the loose ends still remaining.
Possible approach
Students will need to be familiar with the operations introduced in Twisting and Turning:Twist ($x \mapsto x+1$) and Turn ($x \mapsto -\frac1x$).
These notes assume that students will have worked on More Twisting and Turning, and developed a general strategy to get to zero, from any fraction. This problem uses T to represent Twist, and R (for rotate) to represent Turn.
Set the first challenge:
To end up at $\frac{4}{5}$, you can carry out the following sequence of operations: $T,T,T,T,T,R,T$ which could be written more concisely as $T^5RT = \frac45$.
Can you find a sequence of operations that leads to $\frac{9}{10}$?
What about $\frac{23}{24}$
Can you find a sequence of operations that gets from $0$ to the fraction $\frac{n}{n+1}$?
Give students some time to work on this, perhaps using the interactive tool in Getting Started to check their work. Then discuss their strategy and justification for getting fractions of the form $\frac{n}{n+1}$.
Then set the next challenge, asking students to try the following sequences:
$T^2RT$
$T^2RT^2RT$
$T^2RT^2RT^2RT$
What do they notice?
Can they find a way to reach $\frac{1}{10}$?
Can they prove that the pattern will continue?
Can they find a way to reach $\frac{1}{10}$?
Can they prove that the pattern will continue?
For students who have met proof by induction, this could be a good opportunity to use that strategy.
The final part of the problem suggests students look for ways to make any fraction, starting from zero. This is quite challenging; the key questions below might provide a useful prompt.
Key questions
What could you do if you had the function $x \mapsto x-1$, an inverse twist, instead of the original twist function?Can you find a strategy to get from any fraction to zero using an inverse twist and a turn function?
How does that help you get from zero to your chosen fraction using the original twist and turn functions?
Possible extension
Further reading about John Conway's rational tangles can be found in the articles Tangles and Symmetric Tangles.Possible support
Encourage students to be playful and explore using the interactive tool in Getting Started.You may also like
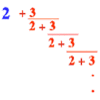
There's a Limit
Explore the continued fraction: 2+3/(2+3/(2+3/2+...)) What do you notice when successive terms are taken? What happens to the terms if the fraction goes on indefinitely?
Not Continued Fractions
Which rational numbers cannot be written in the form x + 1/(y + 1/z) where x, y and z are integers?